Stress-constrained topology optimization
Overview
An interesting, yet challenging problem in topology optimization consists of designing lightweight structures that can withstand applied loading without experiencing local material failure. One of the main challenges associated with this problem is that one must impose a large number of material failure constraints (often thousands or even millions of constraints) to prevent failure at any material point. Although highly relevant for industrial applications, most formulations in the literature are unable to solve this problem in an effective and efficient way. A better understanding the mathematical structure of the stress-constrained problem makes it possible to conceive appropriate numerical solution schemes to solve the problem both effectively and efficiently.
The goal of this research is to investigate the Augmented Lagrangian (AL) method as a numerical optimization technique to solve stress-constrained topology optimization problems. We have proposed AL-based formulations that can handle thousands or even millions of stress constraints and have applied to optimize structures made of either linear or nonlinear materials, in a static or in a dynamic setting, and for various failure criteria, so that we can optimize structures made of a wide range of materials.
The formulations that we have introduced have taken us step closer toward bridging the gap between academic work and industry applications. We are interested in continuing our work on AL-based formulations for stress-constrained topology optimization to extend the range of applications to other types of exciting problems involving multi-physics applications, multi-material structures, geometrically nonlinear problems, and more!
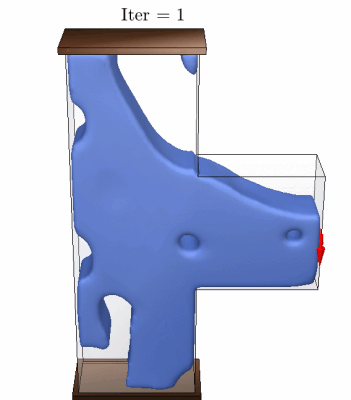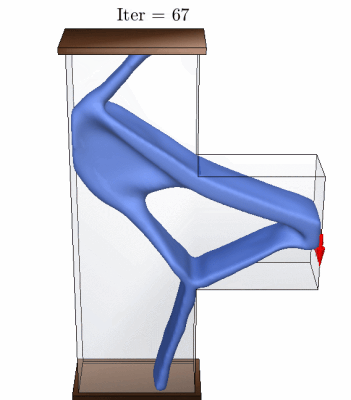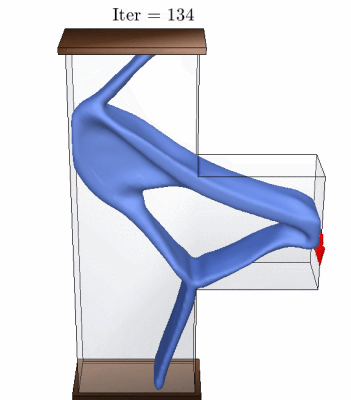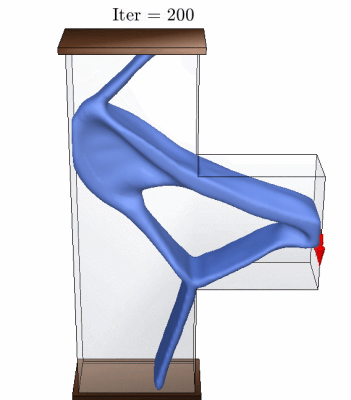
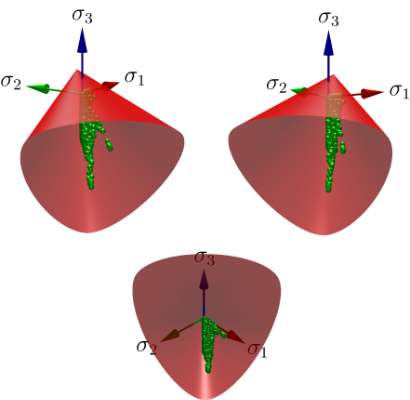
The results above show some of designs we obtained using our AL-based formulation for stress-constrained topology optimization. See more details.
Related publications
Multi-physics topology optimization
Overview
To meet the demands of current industrial applications, it is often the case that a simple mechanical analysis is insufficient to assess the performance of a given system. As stated by Siemens Corporate Technology, "complex industrial problems require solutions that span a multitude of physical phenomena, which often can only be solved using simulation techniques that cross several engineering disciplines."
Following this line of thought, at the COMO laboratory we are interested in pushing the boundaries of topology optimization for applications involving multiple physical phenomena. Thus far, we have developed formulations for thermomechanical topology optimization of multi-material structures, which we have used for the design of support structures for additive manufacturing. Besides this exciting application, our group is interested in exploring a variety of multi-physics problems to design multi-functional structures and structural systems.
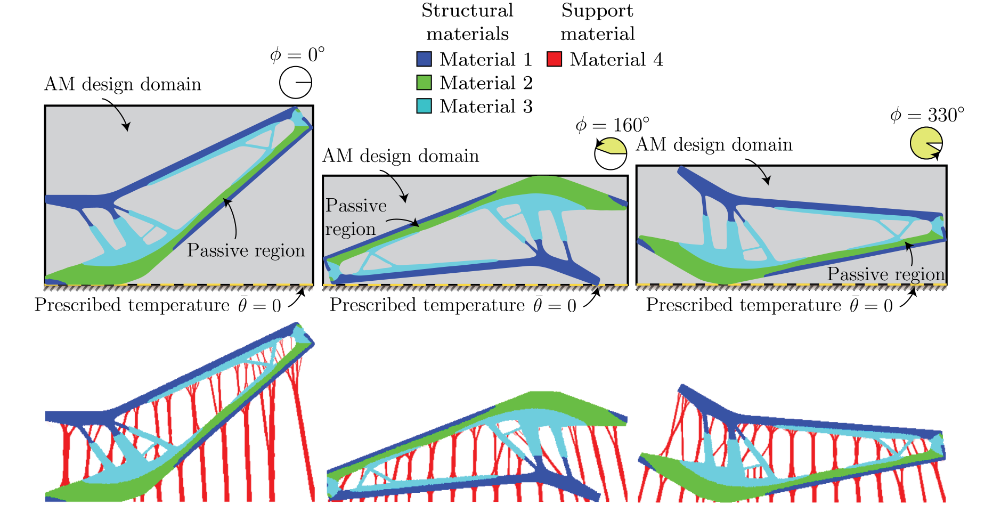
The results shown above, which we obtained as part of a collaboration with researchers at Siemens Corporate Technology, show the optimized topology of an antenna support bracket and the corresponding support structures for additive manufacturing for different print orientations obtained using our multi-material thermomechanical topology optimization formulation. The support structures were designed to better conduct heat away from the antenna support bracket during 3D printing.
Related publications
Microstructure design
Overview
At the COMO Laboratory, we use topology optimization to design macroscale structures but also microscale structures! These types of small-scale structures can be arranged periodically to form composite materials with unprecedented properties that cannot be attained by natural materials. Our objective in this research is to leverage topology optimization to optimize the microstructure of materials (i.e., to design the architecture of the material) for the desired application of interest. We are interested in the design of materials with superior mechanical, thermal, fluidic, or electromagnetic properties.
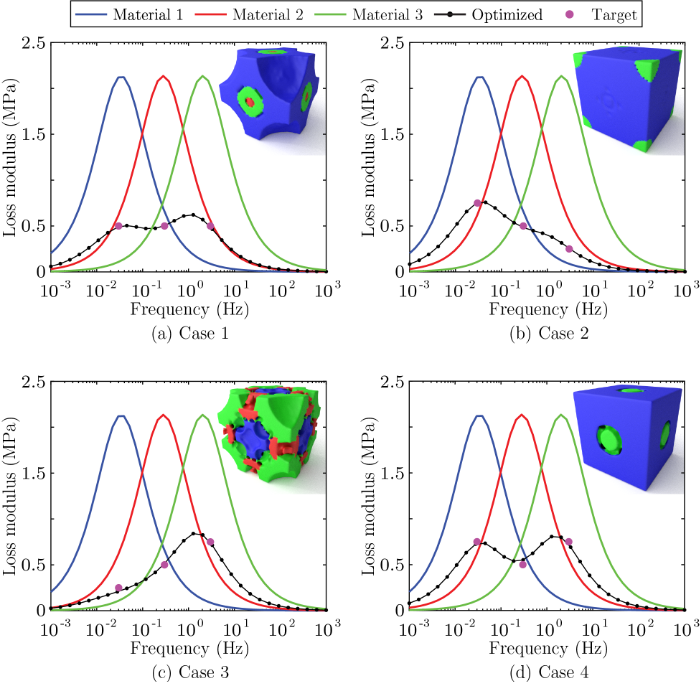
Thus far, we have used our unique approach to solve multi-material topology optimization problems and applied it to design the microstructure of materials with enhanced viscoelastic properties. Specifically, our formulation yields lightweight materials whose loss modulus can be tailored to a specific shape. Below are some results obtained with our formulation which correspond to four-phase viscoelastic materials (3 solid material phases plus a void phase). The optimizer selects the right amount and distribution of each candidate material phase according to the desired viscoelastic response given by the target points.
Related publications
Multi-scale topology optimization
Overview
Nature has taught us that structures made with materials exhibiting multi-scale features can have superior performance as compared to those made of solid, single-scale materials. For instance, our bones are made of hierarchical structures that vary spatially at scales ranging from nanometers to millimeters to ensure their functionality. Another example found in nature is the spider fang, a natural injection needle made of a complex composite material whose microarchitecture varies spatially to form a functionally graded material that is stiff, lightweight, and highly resistant to damage.
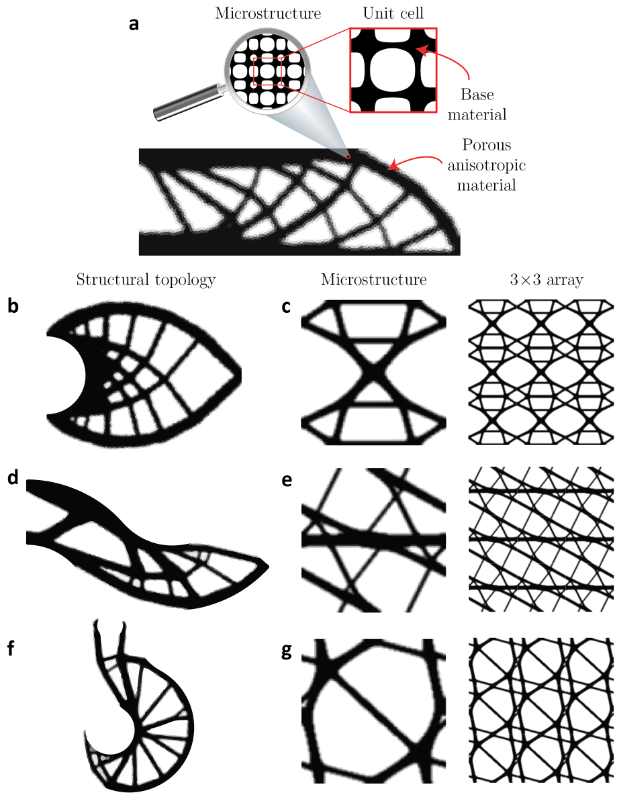
Enabled by additive manufacturing (also known as 3D printing), a promising research area in topology optimization consists of tailoring the material architecture throughout a structural component whose topology is also being optimized. This type of two-scale approach is known as multi-scale topology optimization or concurrent topology optimization and can be used to design structures with unprecedented wight-to-stiffness ratios and damage tolerance. At the COMO Laboratory, we have worked on a formulation for multi-scale topology optimization tailored to achieve lightweight, stiff structural components. Our aim is to find the optimized topology of a structures made of a porous anisotropic material whose topology is also optimized (Figure a). You can see some optimization results obtained with our formulation in Figures b-g. These results clearly show that the topology of the microstructure adapts to the type of macroscopic structure being optimized so that thicker members get aligned with the direction of maximum stress. We are interested in extending this formulation to multi-phase structures and for multi-physics applications!
Additive manufacturing
Overview
Additive manufacturing (AM), also know as 3D printing, has enabled the fabrication of products with unprecedented level of geometrical complexity. The freedom offered by AM makes it a perfect candidate to fabricate components designed via topology optimization. Our group is interested in exploring new technologies for single- and multi-material 3D printing to fabricate complex optimized structures obtained via topology optimization. We are also interested in the utilization of novel active materials to fabricate composite structures which can change their shape after 3D printing, in a new paradigm that is now referred to as 4D printing. We want to understand the properties of existing materials (e.g., piezoelectric, thermoelastic, or ferromagnetic) and their suitability for 3D printing. Another exciting area of interest in our group is the synthesis of self-healing materials which we can use to 3D-print structures with self-healing capabilities.
Computational fracture analysis of rate-dependent materials
Overview
The fracture process in many materials is inherently rate dependent. Rate-dependence can be attributed to bulk-material viscoelasticity, the bond-breakage process in front of the crack tip or a combination of them. Understanding the underlying mechanisms that produce rate dependence in the fracture process is of importance in several industries, including automotive, aeronautical, and civil, among others. In our group, we are interested in gaining a fundamental understanding of rate-dependent fracture process to develop reliable and robust theoretical models of rate-dependent fracture and their corresponding numerical implementation within the framework of the finite element method.
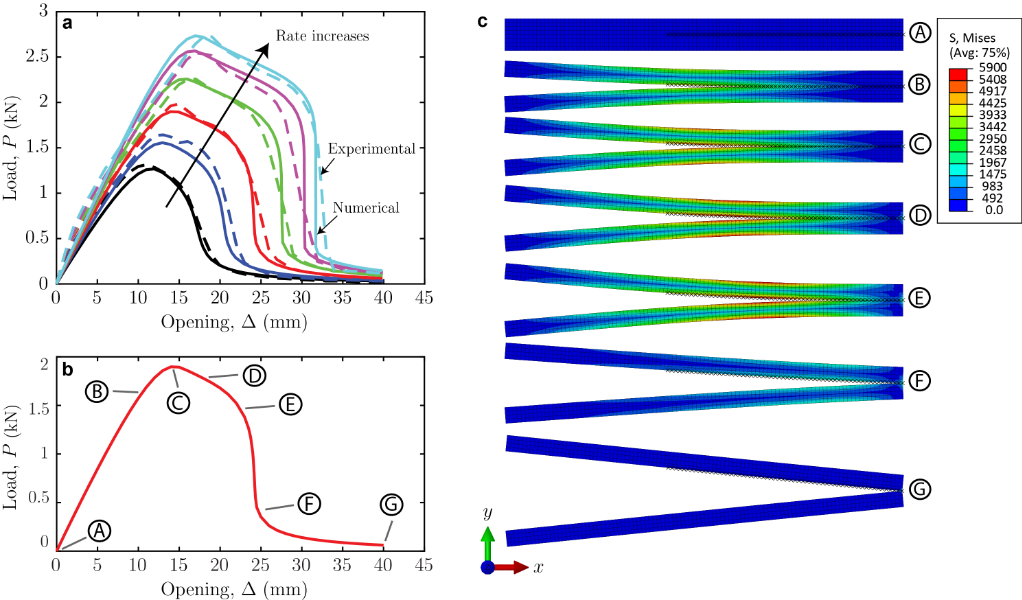
At the COMO Laboratory, we conceived a mathematical model for fracture of rate-dependent materials that is based on fractional calculus, a branch of mathematics that studies differential operators of non-integer order. Enabled by fractional differential operators, the new model can reproduce rate-dependent fracture phenomena for materials with either short- or long-term memory. The figure below shows an example of the results obtained with our fractional calculus-based model, where we analyzed the rate-dependent debonding process of a rubbery interface. The model can reproduce experimental Load vs. Opening curves for load opening rates ranging from 0.01 mm/min to 500 mm/min with a remarkable level of accuracy.
Related publications
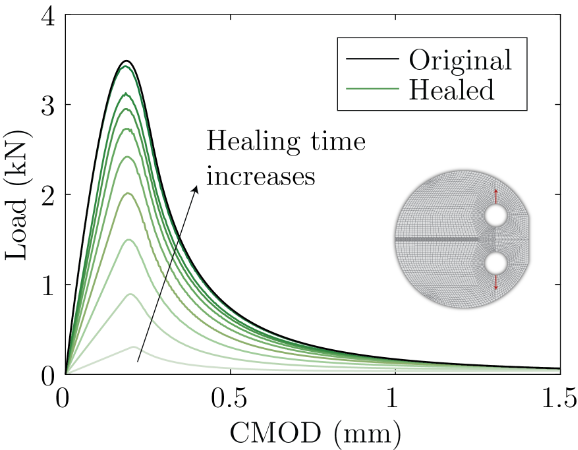
Modeling of fracture and healing of self-healing structures
Overview
Biological tissues such as skin or bones have the inherent ability to heal themselves to recover functionality. Inspired by this ability, scientists have developed synthetic materials that can self-heal, which has opened new avenues toward the design of safer components for applications involving flexible electronics, soft robotics, biomedical devices, among others. For instance, self-healing materials have been used to design strain sensors for soft robotics, soft pneumatic actuators, liquid-metal circuits, and bone replacements, to name a few. Our group is developing new theories to model fracture and healing of components made of self-healing materials. Our computational approach is based on a cohesive zone model that has been enriched with self-healing capabilities. Below are some preliminary results obtained with our cohesive-healing model, which we applied to a disk-shaped compact tension test typically used for fracture testing of asphalt samples.