3D Corbel
Problem description
The 3D model above corresponds to the stress-constrained topology optimization results for the 3D corbel shown below. The optimization results were obtained using 250k regular hexahedral elements on a MATLAB implementation of an augmented Lagrangian-based formulation for topology optimization with local stress constraints. The stress constraints are based on a unified failure function that is able to represent several failure criteria such as von Mises, Drucker–Prager, Tresca, Mohr–Coulomb, Bresler–Pister, and Willam–Warnke.
3D Corbel
Problem description
The 3D model above corresponds to the stress-constrained topology optimization results for the 3D corbel shown below. The optimization results were obtained using 250k regular hexahedral elements on a MATLAB implementation of an augmented Lagrangian-based formulation for topology optimization with local stress constraints. The stress constraints are based on a unified failure function that is able to represent several failure criteria such as von Mises, Drucker–Prager, Tresca, Mohr–Coulomb, Bresler–Pister, and Willam–Warnke.

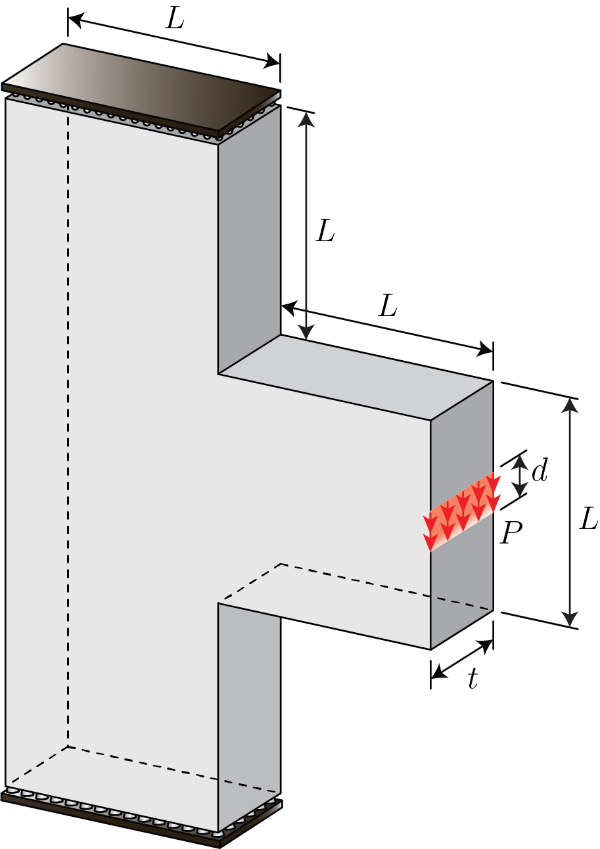
3D Corbel
Problem description
The 3D model above corresponds to the stress-constrained topology optimization results for the 3D corbel shown below. The optimization results were obtained using 250k regular hexahedral elements on a MATLAB implementation of an augmented Lagrangian-based formulation for topology optimization with local stress constraints. The stress constraints are based on a unified failure function that is able to represent several failure criteria such as von Mises, Drucker–Prager, Tresca, Mohr–Coulomb, Bresler–Pister, and Willam–Warnke.
